Want a quick way to find a bunch of prime numbers under some value? This is an oldie but a goodie.

Wowwwww it’s been awhile since I’ve done a blog post. This is because it’s my senior spring at Swarthmore! It’s been a fantastic semester so far. The huge shift from other semesters is that I’m only taking three classes. They are Computer Vision, Theory of Computation, and finally, my buddy Tom and my E90… which hopefully I’ll get to write more about through another blog post. Anyways! I’ve got a decent amount of free time, but that’s largely been sucked up by tennis and hanging with my friends.

However, I did want to keep my blog updated and keep adding to this. It’s really become something I’m pretty happy about it.

The thing I’m going to talk about today is an ancient algorithm called the Sieve of Eratosthenes. You can find the code here if you don’t want to read a little history and about the algorithm.

History of Eratosthenes

This algorithm for finding prime numbers was created by Eratosthenes of Cyrene. You can check out his wiki page right here. Check out the size of that guys head.

He was born in 276 BC and died in 194 BC. He was also apparently a geographer, poet, astronomer, and music theorist. In addition to being a mathematician… so as you can tell, he loved to learn. His work was probably predominantly in the field of geography and astronomy. He was said to be the first person to do the following:

• calculate the circumference of the Earth
• calculate the tilt of the Earth’s axis
• (maybe) accurately calculated the distance between the Earth and the Sun
• invented leap day

In addition to those great accomplishments, he also was tight with Archimedes which is cool. He also at one point became the chief librarian at the Library of Alexandria.

However, sadly, the end of his life was not so glamorous. He got ophthalmia when he became older. Essentially, this is just an inflammation of the eye. However, it can be pretty intense. Unfortunately for our friend Eratosthenes, it did get pretty extreme. He became blind around 195 BC. After becoming blind, he couldn’t read and he became pretty depressed. He ended up starving himself and died at 82 in Alexandria.

But! His name is not forgotten and he contributed in so many ways to get to the level of human experience that we are currently at. He also did a bit of work on prime numbers which is what we’re going to talk about in this blog post.

The beauty behind his simple algorithm for finding prime numbers is really its simplicity. Just staring at the gif and looking briefly at the pseudocode probably let me code it up in maybe 5 minutes. This is not a brag even. Trust me. It’s just that the algorithm is really that simple. So let’s get into that.

Sieve for Finding Prime Numbers

The beauty of this algorithm is that it’s so straight forward. It makes intuitive sense. Some parts get tricky if we optimize, but I’m willing to bet that you can just watch this gif and you’d be able to code up the algorithm. Check it out:

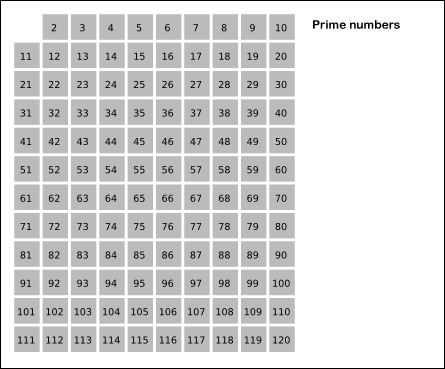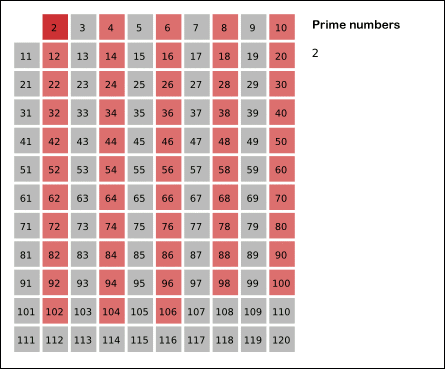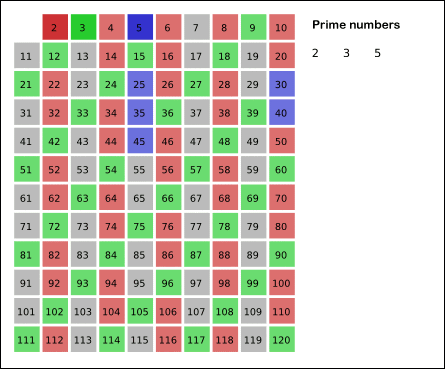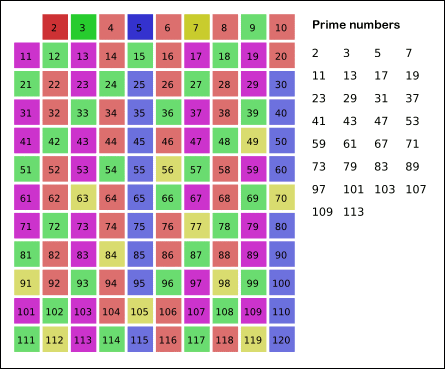
So essentially what you do is just start with an array \([2:upper-lim]\). Then you just start to iterate over the numbers, crossing off the multiples. It’s literally that simple. There are multiple optimizations but the easiest one is probably to start from the number you’re about to find the multiplies at squared, because you know that the smaller multiplies will have already been flagged. This will also help the runtime of the program. You can also start with odd numbers. This is what Eratosthenes actually did. He utilized something called wheel factorization. I don’t really know anything about that.

You can check out the wiki article for the pseudocode.

Asymptotic Runtime

Interestingly enough, the sieve of Eratosthenes is commonly used as a metric for computer performance. The runtime is:

\[O(n \log \log n)\]

This is because the prime harmonic series approaches \(\log \log n\). Essentially, this is similar to the divergence of the sum of the reciprocals for primes. In other words,

\[\sum_{p prime} \frac{1}{p} = \frac{1}{2} + \frac{1}{3} + \frac{1}{5} + \frac{1}{7} + \frac{1}{11} + \cdots = \infty\]

On that tagged wikipedia page, this one, there is a proof showing that the series above grows as least as fast as \(\log \log n\). We can therefore utilize this fact to confirm our asymptotic runtime.

Conclusion

That’s all I’m really going to say about this. I know it wasn’t a particularly long algorithm write up, but it is a different type of algorithm more of a construction algorithm. This idea of a sieve is really nice for coming up with interesting math problems. I’ve had to use it for another question, which hopefully I’ll have time to write about at a later point.

As always, thanks for your time and for reading. Let me know if my code has any improvements to be made.