So while I tried to mainly focus on optimizers, this post kinda splayed out some. It was my first time trying Pyodide and incorporating that logic into my blog. It was my first time using manim, which was exciting because I'm a big fan of the 3Blue1Brown channel. I also introduced quizzes (see AdamW section) for more interactivity. All of this is open source though, so if you have any questions, I'd be flattered if you emailed, but obviously you can just ask ChatGPT / Claude.

Motivating Visualization

Read on to understand the above visualization. My manim skills aren't fantastic so the timing of above could be improved.

Today, we’re going to try and understand as much of this animation as possible. We’ll cover optimizers as a construct, look at an example, take a walk through history (again high level) and then we’ll investigate Muon, which is a more recent optimizer that has been sweeping the community. Note, we will not cover Newton-Schulz iteration or approximation of the SVD calc, but I’m hoping to cover that in another blog post.

Background

nanochat just dropped a couple of weeks ago and one element that I was extremely interested in was muon. It’s a pretty recent state of the art optimizer that has shown competitive performance in training speed challenges.

First of all, if you are not familiar with some of this, you should start with Keller Jordan’s blog that I linked above. He’s the creator of the approach and it’s pretty ingenious. Second of all, if you’re not familiar with linear algebra at all (which is ok), I’d recommend this Little Book of Linear Algebra. I ran through it over the past couple weeks so that I could ensure a strong base / have a refresher for some of the concepts that I haven’t seen since college. You can check out the Jupyter notebooks here.

This post is going to try and take you as close from $0 \to 1$ as possible (one huge benefit of running through the book + lab linked above is my latex got way better. Not going to help me land a job at Anthropic but c’est la vie).

Table of Contents

• Motivating Visualization
• Background
• Table of Contents
• (optional) Reading + Videos
• 1. Deep Learning
• Tour of Popular Optimizers
  • Loss Function
    • Visualization
  • Stochastic Gradient Descent
  • SGD with Momentum
    • Computational Cost of Momentum
    • Variations
  • Adaptive Learning Rates (AdaGrad / RMSProp)
    • AdaGrad (2010)
      • Variations
    • RMSProp (2012)
      • Variations
  • Bias Correction (finally meeting Adam Optimizer, 2015)
    • Comparison so Far
    • Plain English
    • Viz
  • Weight Decay Coupling (the “W” in AdamW, 2017)
    • L2 Regularization
    • Viz
• —– params —–
• Adam / AdamW hyperparams
• —– runs —–
• —– viz —–
• Muon (MomentUm Orthogonalized by Newton-Schulz) (2025)
  • Theory
    • Odd Polynomial Matrix
    • Newton-Schulz Iteration
    • Overview
  • Implementation
• —– params —–
• Adam / AdamW hyperparams
• —– runs —–
• ===== Muon (minimal integration; assumes your run_muon_muonshot handles shape) =====
• —– viz —–
• Muon trace (minimal additional plotting)
• Conclusion

(optional) Reading + Videos

These are a couple of helpful resources for you all to get started. I would actually think that if you’re starting from close to scratch or near scratch (haven’t studied AdamW) then you should probably come back to these after my article.

• Videos
  • This Simple Optimizer Is Revolutionizing How We Train AI (Muon) (p.s. god the amount of clickbaiting people do is just suffocating me… however, this is a good video)
• Reading
  • Muon: An optimizer for hidden layers in neural networks - Keller Jordan
  • Deriving Muon - Jeremy Bernstein
  • Understanding Muon - Laker Newhouse
    • this series (after doing my own research and investigation) is hilariously written. lots of Matrix allusions

1. Deep Learning

I’m not going to take you from the very beginning, but the language of deep learning is basically just… linear algebra.

We have these “deep learning” models that are really neural networks. All that means is that they’re layers of parameters (weights and biases) that take various inputs and make predictions. They normally are affine transformations followed by a (usually) non-linear activation.

Generally, the flow for training in deep learning goes like this:

1. forward pass (feeding data in)
2. loss function (so we know how we did)
3. backward pass (so we know how to adapt)
4. gradient descent (or flavors thereof… where we actually adjust our weights)

There’s fascinating math at all points of this process. However, we’re going to spend the day focusing on step 4 - and specifically on the subset of optimizers. Modern optimizers modify gradients using momentum, adaptive learning rates, etc.

Here is a high level visualization of what’s happening:

Courtesy of me and Claude hammering on manim

Note, that $ \eta $ here is the learning rate.

Tour of Popular Optimizers

Ok the canonical example with optimizers is that we’re basically trying to find the lowest point in a valley. This is assuming our search space is $\mathbb{R}^3$ really but that’s fine for now.

So like let’s take an actual example with the Grand Canyon. Imagine you’re standing on top of the Grand Canyon - how are you going to find the lowest point in the Grand Canyon?

Kudos to Jason Weiss

Now, the optimizer is basically telling us how to walk down that space. It’s obviously a lot easier if we have a topographic map, but we certainly do not in deep learning, and even with the topographic map, it can be tough to search across.

Kudos to DataByYou

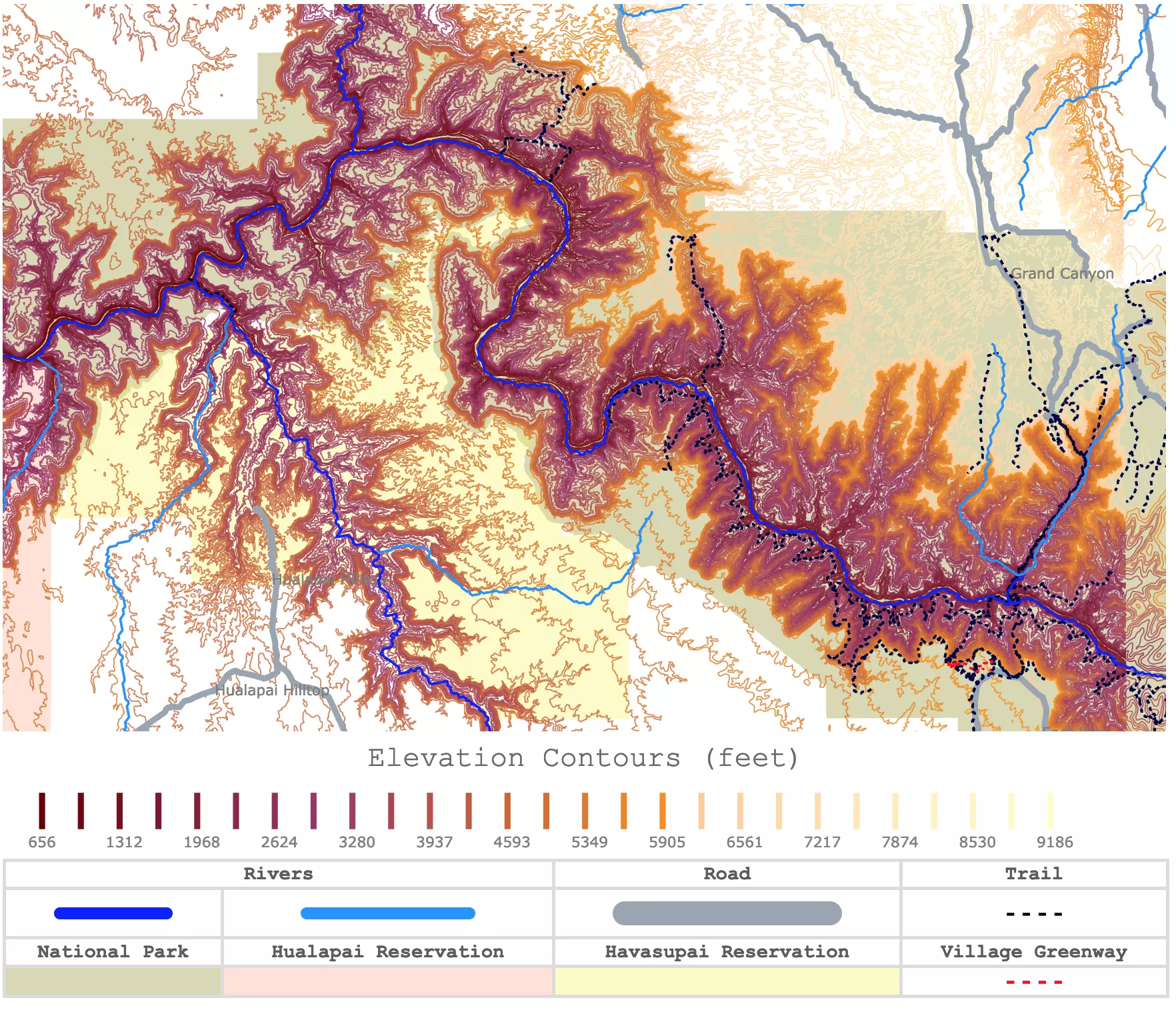
In this analogy, elevation is basically how “wrong” we are. You can think of it as the output of our loss function $L(\hat{y}, y)$. So we compute gradients to determine which direction reduces that loss. However, we still don’t know how big each step would be (the $\eta$ mentioned above) or how to adjust over time or how to avoid getting caught in local minima, etc.

Loss Function

Visualization

I don’t have a loss function that is equivalent to the Grand Canyon (sadly), but we are going to look at the Styblinski Tang function as our example loss function. This isn’t going to be accurate, but imagine that the loss function of our deep learning process is only in 3D and has a shape that can be described by a function. In 2D, the Styblinski Tang function looks like this:

\[\begin{align} f(x,y) &= \frac{1}{2}\sum_{i=1}^{d} \big(x_i^4 - 16x_i^2 + 5x_i \big) \\ f(x,y) &= \frac{1}{2}(x_i^4 - 16x_i^2 + 5x_i ) (y_i^4 - 16y_i^2 + 5y_i ) \end{align}\]

Here’s a visualization of this function:

Courtesy of me and Claude hammering on manim

Stochastic Gradient Descent

Conceptually with standard stochastic gradient descent (SGD), we update our weights so that we move in the opposite direction of the gradient (given gradient points to highest uphill direction).

Mathematically speaking, this is:

\[\theta_{t+1} = \theta_t - \eta \nabla_{\theta} L (\theta_t)\]

SGD works pretty well but it’s far from the best. Think about it back to our Grand Canyon approach. Imagine there are steep stairs but they zig-zag back and forth down the grand canyon. Potentially there is a ramp that is less steep but still more directly gets us to the lowest point in the valley quicker. If our landscape is more dynamic than just a vanilla bowl,that path is almost certainly not straight, and therefore SGD isn’t the most efficient. This is basically what happens to SGD in ravines. There is high curvature in one dimension, but not in another.

Furthermore, this step size for the gradient descent isn’t dynamic enough. Having one step size doesn’t take into nuance the steps per model param / model param derivative that we need to adjust by, so we can overblow our targets.

Here’s an example of where SGD could get caught in a local minima.

Courtesy of me and Claude hammering on manim

And if 3D isn’t really your style (especially given my manima skills are pretty poor). Here’s some Python code that will visualize SGD as a topological 2D portion:

import numpy as np
import matplotlib.pyplot as plt
from itertools import product

def styblinski_tang_fn(x: float, y: float) -> float:
    return 0.5 * ((x**4 - 16 * x**2 + 5 * x) + (y**4 - 16 * y**2 + 5 * y))

def styblinski_tang_grad(x: float, y: float) -> np.ndarray:
    dfx = 2 * x**3 - 16 * x + 2.5
    dfy = 2 * y**3 - 16 * y + 2.5
    return np.array([dfx, dfy], dtype=float)

"""learning params"""
eta = 0.01
steps = 80
theta = np.array([3.5, -3.5], dtype=float)

"""SGD!!! This is the important part here. Implementing the exact math above."""
path = [theta.copy()]
for _ in range(steps):
    grad = styblinski_tang_grad(*theta)
    theta -= eta * grad
    path.append(theta.copy())
path = np.array(path)

"""find stationary points (we can just look at derivative because repeated)"""
roots = np.roots([2.0, 0.0, -16.0, 2.5])
roots = np.real(roots[np.isreal(roots)])          # keep real roots
"""this is basically using second derivative to determine minima"""
minima_1d = [r for r in roots if (6*r*r - 16) > 0]  # two minima
local_minima_2d = np.array(list(product(minima_1d, repeat=2)), dtype=float)
vals = np.array([styblinski_tang_fn(x, y) for x, y in local_minima_2d])
gmin_idx = np.argmin(vals)
gmin_pt = local_minima_2d[gmin_idx]
gmin_val = vals[gmin_idx]

"""viz"""
x = y = np.linspace(-5, 5, 300)
X, Y = np.meshgrid(x, y)
Z = styblinski_tang_fn(X, Y)
plt.figure(figsize=(7, 6))
cs = plt.contour(X, Y, Z, levels=40, cmap="viridis", alpha=0.85)
plt.clabel(cs, inline=True, fmt="%.0f", fontsize=8)
plt.plot(path[:, 0], path[:, 1], 'r.-', label='GD Path', zorder=2)
plt.scatter(path[0, 0], path[0, 1], color='orange', s=80, label='Start', zorder=3)
plt.scatter(path[-1, 0], path[-1, 1], color='blue', s=80, label='End', zorder=3)
mask = np.ones(len(local_minima_2d), dtype=bool)
mask[gmin_idx] = False
if np.any(mask):
    plt.scatter(local_minima_2d[mask, 0], local_minima_2d[mask, 1],
                marker='v', s=120, edgecolor='k', facecolor='white',
                label='Local minima', zorder=4)
plt.scatter(gmin_pt[0], gmin_pt[1], marker='*', s=220, edgecolor='k',
            facecolor='gold', label=f'Global min ({gmin_pt[0]:.4f}, {gmin_pt[1]:.4f})\n f={gmin_val:.4f}', zorder=5)
plt.title("Gradient Descent on Styblinski–Tang: Local vs Global Minima")
plt.xlabel("x"); plt.ylabel("y"); plt.legend(loc='upper right'); plt.grid(alpha=0.3); plt.tight_layout();
plt.show()

SGD with Momentum

So the natural progression is how can we do better than normal SGD.

This idea has been around forever (1964) compared to Muon which is basically 2025. Boris Polyak introduced momentum with physical intuition. If you roll a heavy ball down a hill and there are valleys, it doesn’t get trapped in a local minima. It has momentum to carry it over local minimum which helps find a global min.

Mathematically, it’s a pretty simple extension from our previous. The general idea is that now we have two equations governing how we update our parameters:

\[\begin{align} v_{t+1} &= \beta v_t - \eta \nabla_{\theta} L (\theta_{t}) \\ \theta_{t+1} &= \theta_{t} + v_{t+1} \end{align}\]

We’ve got some new parameters, so let’s define those:

• $v_{t}$ - is the “velocity”, it’s the accumulated gradient basically our physical momentum
• $\beta$ - is the “momentum coefficient”. controls how much history we remember and how much we want to propagate
• $\eta$ - is still our learning rate

A key insight is that if you take $\beta \to 0$ and substitute $v_{t+1}$ then our whole thing falls back to SGD (which is good).

A core paradigm shift here was that this was the first time gradient descent carried with it the notion of memory. It’s a bit more stateful.

Once again, a 3D version, and a 2D version.

Courtesy of me and Claude hammering on manim

And the 2D visualization:

import numpy as np
import matplotlib.pyplot as plt
from itertools import product

def styblinski_tang_fn(x: float, y: float) -> float:
    return 0.5 * ((x**4 - 16 * x**2 + 5 * x) + (y**4 - 16 * y**2 + 5 * y))

def styblinski_tang_grad(x: float, y: float) -> np.ndarray:
    dfx = 2 * x**3 - 16 * x + 2.5
    dfy = 2 * y**3 - 16 * y + 2.5
    return np.array([dfx, dfy], dtype=float)

def stationary_points_and_global_min():
    roots = np.roots([2.0, 0.0, -16.0, 2.5])
    roots = np.real(roots[np.isreal(roots)])
    minima_1d = [r for r in roots if (6*r*r - 16) > 0]
    mins2d = np.array(list(product(minima_1d, repeat=2)), dtype=float)
    vals = np.array([styblinski_tang_fn(x, y) for x, y in mins2d])
    gidx = np.argmin(vals)
    return mins2d, mins2d[gidx], vals[gidx]

def run_sgd(theta0, eta=0.02, steps=1200):
    theta = np.array(theta0, float)
    path = [theta.copy()]
    for _ in range(steps):
        theta -= eta * styblinski_tang_grad(*theta)
        path.append(theta.copy())
    return np.array(path)

"""
again, re-call beta is our momentum coefficient
eta is still our learning rate
extension: Nesterov Momentum
"""
def run_momentum(theta0, eta=0.02, beta=0.90, steps=1200):
    theta = np.array(theta0, float)
    v = np.zeros_like(theta)
    path = [theta.copy()]
    for _ in range(steps):
        grad = styblinski_tang_grad(*theta)
        v = beta * v - eta * grad
        theta = theta + v
        path.append(theta.copy())
    return np.array(path)

"""params"""
theta_start = np.array([4.1, 4.5], dtype=float)
eta = 0.02
beta = 0.90
steps = 1200
use_nesterov = False  # flip to True to experiment

sgd_path = run_sgd(theta_start, eta=eta, steps=steps)
mom_path = run_momentum(theta_start, eta=eta, beta=beta, steps=steps)
mins2d, gmin_pt, gmin_val = stationary_points_and_global_min()

"""viz"""
x = y = np.linspace(-5, 5, 400)
X, Y = np.meshgrid(x, y)
Z = styblinski_tang_fn(X, Y)

plt.figure(figsize=(8, 7))
cs = plt.contour(X, Y, Z, levels=50, cmap="viridis", alpha=0.85)
plt.clabel(cs, inline=True, fmt="%.0f", fontsize=7)
plt.plot(sgd_path[:, 0], sgd_path[:, 1], 'r.-', lw=1.5, ms=3, label='SGD')
plt.plot(mom_path[:, 0], mom_path[:, 1], 'b.-', lw=1.5, ms=3,
         label=f'Momentum (β={beta}, nesterov={use_nesterov})')
plt.scatter(sgd_path[0, 0], sgd_path[0, 1], c='orange', s=80, label='Start', zorder=3)
plt.scatter(sgd_path[-1, 0], sgd_path[-1, 1], c='red', s=70, label='SGD End', zorder=3)
plt.scatter(mom_path[-1, 0], mom_path[-1, 1], c='blue', s=70, label='Momentum End', zorder=3)
vals = np.array([styblinski_tang_fn(x0, y0) for x0, y0 in mins2d])
mask = np.ones(len(mins2d), dtype=bool)
mask[np.argmin(vals)] = False
if np.any(mask):
    plt.scatter(mins2d[mask, 0], mins2d[mask, 1],
                marker='v', s=120, edgecolor='k', facecolor='white',
                label='Local minima', zorder=4)
plt.scatter(gmin_pt[0], gmin_pt[1], marker='*', s=220, edgecolor='k',
            facecolor='gold', label=f'Global min ({gmin_pt[0]:.4f}, {gmin_pt[1]:.4f})\n f={gmin_val:.4f}', zorder=5)

plt.title("SGD vs Momentum on Styblinski–Tang: Escaping a Local Minimum")
plt.xlabel("x"); plt.ylabel("y")
plt.legend(loc='lower right'); plt.grid(alpha=0.3); plt.tight_layout()
plt.show()

Computational Cost of Momentum

So while momentum is great and improves training, let’s look at the change. In SGD, we have:

• for each parameter $\theta_i$:
  • parameter itself
  • gradient $\nabla_{\theta_{i}} L$

But now that we’re carrying around velocity $v_i$ for each parameter, we store:

• memory wise:
  • one extra tensor the same size as $\theta$ (i.e. the same number of parameters we have )
• comp wise:
  • this is relatively inexpensive given it’s basically one more computation to make
  • but a good callout is that it’s not free

Again, even if you didn’t look at all at the code above, and just ran it, see this part:

def run_momentum(theta0, eta=0.02, beta=0.90, steps=1200):
    theta = np.array(theta0, float)
    v = np.zeros_like(theta)
    path = [theta.copy()]
    for _ in range(steps):
        grad = styblinski_tang_grad(*theta)
        v = beta * v - eta * grad
        theta = theta + v
        path.append(theta.copy())
    return np.array(path)

That v didn’t exist before with standard SGD.

This is a general tradeoff that we’ll need to think about optimizer design. We need to be thinking about this on a massive magnitude of training and that each operation has significant impact leading to real $ signs.

Variations

I won’t go into these in detail, but as with everything, there are numerous variations.

• Nesterov momentum (a.k.a NAG)

Adaptive Learning Rates (AdaGrad / RMSProp)

Great, so momentum is going to help us smooth learning. The next area of improvement was for people to focus on $\eta$. It sucks that it’s the same for every parameter, so the whole notion was that we want to have our learning rate be adaptive per parameter.

This section is where the math starts to get a bit more interesting.

AdaGrad (2010)

Adaptive gradient came first. Here’s the original paper written in 2010 by John Duchi, Elad Hazan, and Yoram Singer.

The general idea is:

• we keep track of how large each parameter’s past gradients have been
• we use the history to scale down updates for params that have seen a lot of gradient action

So the core idea here is that we’re going to track the sum of each parameters squared gradients over time. And this helps a ton of things with things like vanishing and exploding gradients (which actually was also an annoyance with Teaching a Computer How to Write.

In other words,

\[r_{t,i} = \sum_{k=1}^t g_{k,i}^2\]

So basically $r_{t,i}$ for the $i$th parameter at time $t$ is going to tell you how much more or less “energy”.

Then our update rule rescales the learning rate for each param coordinates:

\[\theta_{t+1, i} = \theta_{t,i} - \frac{\eta}{\sqrt{r_{t,i}} + \varepsilon} g_{t,i}\]

This can be written in a vectorized format like:

\[\theta_{t+1} = \theta_{t} - \eta D_{t}^{-1/2} g_{t}\]

where $D_t = \text{diag}(r_t)$ and each diagonal element corresponds to one coordinate’s cumulative gradient magnitude. So we’re basically embedding the $i$ into the shape of the vectors and dimension.

Again, DL loves big matrices.

I am not going to try and do a 3D visualization given those take me awhile to get to an acceptable place.

import numpy as np
import matplotlib.pyplot as plt
from sympy import Matrix, pprint, init_printing
from itertools import product
from IPython.display import display
init_printing(use_unicode=True)

def styblinski_tang_fn(x: float, y: float) -> float:
    return 0.5 * ((x**4 - 16 * x**2 + 5 * x) + (y**4 - 16 * y**2 + 5 * y))

def styblinski_tang_grad(x: float, y: float) -> np.ndarray:
    dfx = 2 * x**3 - 16 * x + 2.5
    dfy = 2 * y**3 - 16 * y + 2.5
    return np.array([dfx, dfy], dtype=float)

def stationary_points_and_global_min():
    roots = np.roots([2.0, 0.0, -16.0, 2.5])
    roots = np.real(roots[np.isreal(roots)])
    minima_1d = [r for r in roots if (6*r*r - 16) > 0]
    mins2d = np.array(list(product(minima_1d, repeat=2)), dtype=float)
    vals = np.array([styblinski_tang_fn(x, y) for x, y in mins2d])
    gidx = np.argmin(vals)
    return mins2d, mins2d[gidx], vals[gidx]

def run_sgd(theta0, eta=0.02, steps=1200):
    theta = np.array(theta0, float)
    path = [theta.copy()]
    for _ in range(steps):
        theta -= eta * styblinski_tang_grad(*theta)
        path.append(theta.copy())
    return np.array(path)

def run_momentum(theta0, eta=0.02, beta=0.90, steps=1200):
    theta = np.array(theta0, float)
    v = np.zeros_like(theta)
    path = [theta.copy()]
    for _ in range(steps):
        grad = styblinski_tang_grad(*theta)
        v = beta * v - eta * grad
        theta = theta + v
        path.append(theta.copy())
    return np.array(path)

def run_adagrad(theta0, eta=0.40, eps=1e-8, steps=1200):
    """
    r_t <- r_{t-1} + g_t^2
    theta <- theta - (eta / (sqrt(r_t) + eps)) * g_t
    """
    theta = np.array(theta0, float)
    r = np.zeros_like(theta)         
    path = [theta.copy()]
    for step in range(steps):
        g = styblinski_tang_grad(*theta)
        r = r + g * g
        lr = eta / (np.sqrt(r) + eps) # elementwise effective LR
        if step % 100 == 0 and step < 600:
            D = np.diag(r)
            print(f"\nStep {step}:  Dt = diag(r_step)")
            display(Matrix(D))
        if step == steps - 1:
            D = np.diag(r)
            print(f"\nFinal Step {step}:  Dt = diag(r_step)")
            display(Matrix(D))
        theta = theta - lr * g
        path.append(theta.copy())
    return np.array(path)

"""params"""
theta_start = np.array([4.1, 4.5], dtype=float)
eta = 0.02
beta = 0.90
steps = 1200
eta_adagrad = 0.40
eps_adagrad = 1e-8

sgd_path = run_sgd(theta_start, eta=eta, steps=steps)
mom_path = run_momentum(theta_start, eta=eta, beta=beta, steps=steps)
ada_path = run_adagrad(theta_start, eta=eta_adagrad, eps=eps_adagrad, steps=steps)
mins2d, gmin_pt, gmin_val = stationary_points_and_global_min()

"""viz"""
x = y = np.linspace(-5, 5, 400)
X, Y = np.meshgrid(x, y)
Z = styblinski_tang_fn(X, Y)

plt.figure(figsize=(8, 7))
cs = plt.contour(X, Y, Z, levels=50, alpha=0.85)   # (kept close; removed explicit cmap for portability)
plt.clabel(cs, inline=True, fmt="%.0f", fontsize=7)

plt.plot(sgd_path[:, 0], sgd_path[:, 1], 'r.-', lw=1.5, ms=3, label='SGD')
plt.plot(mom_path[:, 0], mom_path[:, 1], 'b.-', lw=1.5, ms=3,
         label=f'Momentum (β={beta})')
plt.plot(ada_path[:, 0], ada_path[:, 1], 'g.-', lw=1.5, ms=3,
         label=f'AdaGrad (η₀={eta_adagrad})')

plt.scatter(sgd_path[0, 0], sgd_path[0, 1], c='orange', s=80, label='Start', zorder=3)
plt.scatter(sgd_path[-1, 0], sgd_path[-1, 1], c='red', s=70, label='SGD End', zorder=3)
plt.scatter(mom_path[-1, 0], mom_path[-1, 1], c='blue', s=70, label='Momentum End', zorder=3)
plt.scatter(ada_path[-1, 0], ada_path[-1, 1], c='green', s=70, label='AdaGrad End', zorder=3)

vals = np.array([styblinski_tang_fn(x0, y0) for x0, y0 in mins2d])
mask = np.ones(len(mins2d), dtype=bool)
mask[np.argmin(vals)] = False
if np.any(mask):
    plt.scatter(mins2d[mask, 0], mins2d[mask, 1],
                marker='v', s=120, edgecolor='k', facecolor='white',
                label='Local minima', zorder=4)
plt.scatter(gmin_pt[0], gmin_pt[1], marker='*', s=220, edgecolor='k',
            facecolor='gold', label=f'Global min ({gmin_pt[0]:.4f}, {gmin_pt[1]:.4f})\n f={gmin_val:.4f}', zorder=5)

plt.title("SGD vs Momentum vs AdaGrad on Styblinski–Tang")
plt.xlabel("x"); plt.ylabel("y")
plt.legend(loc='lower right'); plt.grid(alpha=0.3); plt.tight_layout()
plt.show()

Variations

Arguably, RMSProp is a deviation of AdaGrad, but… i decided to split it out given how talked about RMSProp is.

However, similar to AdaGrad, there’s also

• AdaDelta
  • basically does an exponential weighted average

RMSProp (2012)

RMSProp, or Root Mean Square Propagation, allows the effective learning rate to increase or decrease. It cuts away from the effeective LR monotonically shrinking.

Confusingly but importantly, RMSProp is identical to AdaDelta just withohut the running average for parameter updates.

The whole notion of RMSProp is that we keep an exponential weighted moving average (EMA) of recent gradients per parameter.

We scale the raw gradient by the inverse root of that EMA.

In other words,

\[\begin{align} s_t &= \rho s_{t-1} + (1-\rho) g_t^2 \\ \theta_{t+1} &= \theta_t - \eta \frac{g_t}{\sqrt{s_t} + \varepsilon} \end{align}\]

Sometimes people use $\beta$ instead of $\rho$. But here is what these mean:

• $s_t$ - accumulated moving average of squared gradients at time $t$
• $\rho$ - the decay rate, typically between 0.9 and 0.99
• $g(t)$ - still represents our gradient at time $t$

And once again, for matrix math, similar to AdaGrad we can play a similar game with vectorizing it:

\(\theta_{t+1} = \theta_{t} - \eta \tilde{D}_t^{-\frac{1}{2}} g_t\) where \(\tilde{D}_t = \text{diag}(s_t + \varepsilon)\)

So the total result is that we have large, consistently-steep coords get downscaled, and quiet coords get a healthier step. By using a moving window, step sizes don’t vanish over time.

The EMA is meant to focus on recent gradients, and maintains steady effective learning rate while preventing premature decay. With AdaGrad, effective LR monotonically shrinks and can stall on long runs.

Again, I am not going to try and do a 3D visualization given those take me awhile to get to an acceptable place.

import numpy as np
import matplotlib.pyplot as plt
from itertools import product
from sympy import Matrix
from IPython.display import display

def styblinski_tang_fn(x: float, y: float) -> float:
    return 0.5 * ((x**4 - 16 * x**2 + 5 * x) + (y**4 - 16 * y**2 + 5 * y))


def styblinski_tang_grad(x: float, y: float) -> np.ndarray:
    dfx = 2 * x**3 - 16 * x + 2.5
    dfy = 2 * y**3 - 16 * y + 2.5
    return np.array([dfx, dfy], dtype=float)


def stationary_points_and_global_min():
    roots = np.roots([2.0, 0.0, -16.0, 2.5])
    roots = np.real(roots[np.isreal(roots)])
    minima_1d = [r for r in roots if (6 * r * r - 16) > 0]
    mins2d = np.array(list(product(minima_1d, repeat=2)), dtype=float)
    vals = np.array([styblinski_tang_fn(x, y) for x, y in mins2d])
    gidx = np.argmin(vals)
    return mins2d, mins2d[gidx], vals[gidx]


def run_sgd(theta0, eta=0.02, steps=1200):
    theta = np.array(theta0, float)
    path = [theta.copy()]
    for _ in range(steps):
        theta -= eta * styblinski_tang_grad(*theta)
        path.append(theta.copy())
    return np.array(path)


def run_momentum(theta0, eta=0.02, beta=0.90, steps=1200):
    theta = np.array(theta0, float)
    v = np.zeros_like(theta)
    path = [theta.copy()]
    for _ in range(steps):
        g = styblinski_tang_grad(*theta)
        v = beta * v - eta * g
        theta = theta + v
        path.append(theta.copy())
    return np.array(path)


def run_adagrad(theta0, eta=0.40, eps=1e-8, steps=1200):
    theta = np.array(theta0, float)
    r = np.zeros_like(theta)
    path = [theta.copy()]
    for _ in range(steps):
        g = styblinski_tang_grad(*theta)
        r = r + g * g
        lr_eff = eta / (np.sqrt(r) + eps)
        theta = theta - lr_eff * g
        path.append(theta.copy())
    return np.array(path)

def run_rmsprop(theta0, eta=1e-2, rho=0.9, eps=1e-8, steps=1200):
    """
    s_t = rho * s_{t-1} + (1 - rho) * g_t^2
    theta <- theta - eta * g_t / (sqrt(s_t) + eps)
    """
    theta = np.array(theta0, float)
    s = np.zeros_like(theta)
    path = [theta.copy()]
    for step in range(steps):
        g = styblinski_tang_grad(*theta)
        s = rho * s + (1 - rho) * (g * g)
        if step % 100 == 0 and step < 600:
            S = np.diag(s)
            print(f"\nStep {step}:  s_t (EMA of squared gradients)")
            display(Matrix(S))
        if step == steps - 1:
            S = np.diag(s)
            print(f"\nFinal Step {step}:  s_t (EMA of squared gradients)")
            display(Matrix(S))
        theta = theta - eta * g / (np.sqrt(s) + eps)
        path.append(theta.copy())
    return np.array(path)

def run_rmsprop_centered(theta0, eta=1e-2, rho=0.9, eps=1e-8, steps=1200):
    """
    m_t = rho * m_{t-1} + (1 - rho) * g_t
    s_t = rho * s_{t-1} + (1 - rho) * g_t^2
    denom = sqrt(s_t - m_t^2) + eps   # variance-based
    """
    theta = np.array(theta0, float)
    m = np.zeros_like(theta)
    s = np.zeros_like(theta)
    path = [theta.copy()]
    for _ in range(steps):
        g = styblinski_tang_grad(*theta)
        m = rho * m + (1 - rho) * g
        s = rho * s + (1 - rho) * (g * g)
        denom = np.sqrt(np.maximum(s - m * m, 0.0)) + eps
        theta = theta - eta * g / denom
        path.append(theta.copy())
    return np.array(path)


theta_start = np.array([4.1, 4.5], dtype=float)
steps = 1200

eta_sgd = 0.02
eta_mom, beta = 0.02, 0.90
eta_adagrad = 0.40
eta_rms, rho, eps = 1e-2, 0.9, 1e-8
eta_rms_c = 1e-2

sgd_path = run_sgd(theta_start, eta=eta_sgd, steps=steps)
mom_path = run_momentum(theta_start, eta=eta_mom, beta=beta, steps=steps)
ada_path = run_adagrad(theta_start, eta=eta_adagrad, steps=steps)
rms_path = run_rmsprop(theta_start, eta=eta_rms, rho=rho, eps=eps, steps=steps)
rmsc_path = run_rmsprop_centered(theta_start, eta=eta_rms_c, rho=rho, eps=eps, steps=steps)

mins2d, gmin_pt, gmin_val = stationary_points_and_global_min()

x = y = np.linspace(-5, 5, 400)
X, Y = np.meshgrid(x, y)
Z = styblinski_tang_fn(X, Y)

plt.figure(figsize=(9, 8))
cs = plt.contour(X, Y, Z, levels=50, alpha=0.85)
plt.clabel(cs, inline=True, fmt="%.0f", fontsize=7)

plt.plot(sgd_path[:, 0], sgd_path[:, 1], '.-', lw=1.2, ms=3, label='SGD')
plt.plot(mom_path[:, 0], mom_path[:, 1], '.-', lw=1.2, ms=3, label=f'Momentum (β={beta})')
plt.plot(ada_path[:, 0], ada_path[:, 1], '.-', lw=1.2, ms=3, label='AdaGrad')
plt.plot(rms_path[:, 0], rms_path[:, 1], '.-', lw=1.2, ms=3, label=f'RMSProp (ρ={rho})')
plt.plot(rmsc_path[:, 0], rmsc_path[:, 1], '.-', lw=1.2, ms=3, label='RMSProp (centered)')

plt.scatter(sgd_path[0, 0], sgd_path[0, 1], s=80, label='Start', zorder=3)
plt.scatter(sgd_path[-1, 0], sgd_path[-1, 1], s=60, label='SGD End', zorder=3)
plt.scatter(mom_path[-1, 0], mom_path[-1, 1], s=60, label='Momentum End', zorder=3)
plt.scatter(ada_path[-1, 0], ada_path[-1, 1], s=60, label='AdaGrad End', zorder=3)
plt.scatter(rms_path[-1, 0], rms_path[-1, 1], s=60, label='RMSProp End', zorder=3)
plt.scatter(rmsc_path[-1, 0], rmsc_path[-1, 1], s=60, label='RMSProp (centered) End', zorder=3)

vals = np.array([styblinski_tang_fn(x0, y0) for x0, y0 in mins2d])
mask = np.ones(len(mins2d), dtype=bool)
mask[np.argmin(vals)] = False
if np.any(mask):
    plt.scatter(mins2d[mask, 0], mins2d[mask, 1],
                marker='v', s=120, edgecolor='k', facecolor='white',
                label='Local minima', zorder=4)
plt.scatter(gmin_pt[0], gmin_pt[1], marker='*', s=220, edgecolor='k',
            facecolor='gold', label=f'Global min ({gmin_pt[0]:.4f}, {gmin_pt[1]:.4f})\n f={gmin_val:.4f}', zorder=5)

plt.title("SGD vs Momentum vs AdaGrad vs RMSProp (and Centered) on Styblinski–Tang")
plt.xlabel("x")
plt.ylabel("y")
plt.legend(loc='lower right')
plt.grid(alpha=0.3)
plt.tight_layout()
plt.show()

Again, the important code part is here:

def run_rmsprop(theta0, eta=1e-2, rho=0.9, eps=1e-8, steps=1200):
    """
    s_t = rho * s_{t-1} + (1 - rho) * g_t^2
    theta <- theta - eta * g_t / (sqrt(s_t) + eps)
    """
    theta = np.array(theta0, float)
    s = np.zeros_like(theta)
    path = [theta.copy()]
    for step in range(steps):
        g = styblinski_tang_grad(*theta)
        s = rho * s + (1 - rho) * (g * g)
        if step % 100 == 0 and step < 600:
            S = np.diag(s)
            print(f"\nStep {step}:  s_t (EMA of squared gradients)")
            display(Matrix(S))
        if step == steps - 1:
            S = np.diag(s)
            print(f"\nFinal Step {step}:  s_t (EMA of squared gradients)")
            display(Matrix(S))
        theta = theta - eta * g / (np.sqrt(s) + eps)
        path.append(theta.copy())
    return np.array(path)

Variations

• RMSProp (centered)

Bias Correction (finally meeting Adam Optimizer, 2015)

RMSProp is fantastic but still subject to getting caught in local minima.

Ok finally in 2015 people introduced Adam. This is basically marrying the momentum portions along with the utilization of the first two moments from RMSProp / AdaGrad. However, a key introduced is bias-correcting the EMAs because they start at zero and are biased early. Our update uses the direction $\hat{m}_t$ and the scale $\sqrt{\hat{v_t}}$.

Mathematically, we now have:

• momentum part (exp avg of raw gradients, our first moment (i.e. understanding magnitude of gradient updates)) \(m_t = \beta_1 m_{t-1} + (1-\beta_1) g_t\)
• rms prop part (exp avg of squared gradients, our second moment (i.e. understanding energy / dispersion of gradient updates)) \(v_t = \beta_2 v_{t-1} + (1 - \beta_2) g_t^2\)
• bias correction part (new) - getting around the fact that both are starting from 0, so divde by $ 1 - \beta_i^t $ \(\hat{m}_t = \frac{m_t}{1- \beta_1^t} \qquad \hat{v}_t = \frac{v_t}{1-\beta_2^t}\)

with our final update being:

\[\theta_{t+1} = \theta_t - \eta \frac{\hat{m_t}}{\sqrt{\hat{v_t}}+\varepsilon}\]

Again, same thing with the vectorization, we’re always just modifying our $D$ matrix:

\[\theta_{t+1} = \theta_t - \eta D_{t}^{-\frac{1}{2}}\hat{m}_t, \quad D_t = \text{diag}(\hat{v}_t + \varepsilon)\]

Comparison so Far

I had ChatGPT create this table which does a good job of understanding the nuances between:

Optimizer	Tracks mean of gradients?	Tracks mean of squared gradients?	Bias correction?	Update uses
Momentum (Polyak)	✅ $m_t = \beta m_{t-1} + (1-\beta) g_t$	❌	❌	$ \theta_{t+1} = \theta_t - \eta m_t $
RMSProp (Hinton)	❌	✅ $s_t = \rho s_{t-1} + (1-\rho) g_t^2$	❌	$ \theta_{t+1} = \theta_t - \eta \dfrac{g_t}{\sqrt{s_t}+\varepsilon} $
Adam (Kingma & Ba)	✅ $m_t = \beta_1 m_{t-1} + (1-\beta_1) g_t$	✅ $v_t = \beta_2 v_{t-1} + (1-\beta_2) g_t^2$	✅ divides by (1-\beta^t)	$ \theta_{t+1} = \theta_t - \eta \dfrac{\hat m_t}{\sqrt{\hat v_t}+\varepsilon} $

Plain English

My understanding in plain english in how each step affects this:

• SGD - size of gradient is taken into account
• SGD with momentum - adds smoothing with momentum (introduces $\hat{m}_t$)
• RMSProp - adds scaling for recent average squared gradients vs older ones
• Adam - bias correction to fix underestimation at early timesteps

Viz

import numpy as np
import matplotlib.pyplot as plt
from itertools import product
from sympy import Matrix
from IPython.display import display

def styblinski_tang_fn(x: float, y: float) -> float:
    return 0.5 * ((x**4 - 16 * x**2 + 5 * x) + (y**4 - 16 * y**2 + 5 * y))


def styblinski_tang_grad(x: float, y: float) -> np.ndarray:
    dfx = 2 * x**3 - 16 * x + 2.5
    dfy = 2 * y**3 - 16 * y + 2.5
    return np.array([dfx, dfy], dtype=float)


def stationary_points_and_global_min():
    roots = np.roots([2.0, 0.0, -16.0, 2.5])
    roots = np.real(roots[np.isreal(roots)])
    minima_1d = [r for r in roots if (6 * r * r - 16) > 0]
    mins2d = np.array(list(product(minima_1d, repeat=2)), dtype=float)
    vals = np.array([styblinski_tang_fn(x, y) for x, y in mins2d])
    gidx = np.argmin(vals)
    return mins2d, mins2d[gidx], vals[gidx]


def run_sgd(theta0, eta=0.02, steps=1200):
    theta = np.array(theta0, float)
    path = [theta.copy()]
    for _ in range(steps):
        theta -= eta * styblinski_tang_grad(*theta)
        path.append(theta.copy())
    return np.array(path)


def run_momentum(theta0, eta=0.02, beta=0.90, steps=1200):
    theta = np.array(theta0, float)
    v = np.zeros_like(theta)
    path = [theta.copy()]
    for _ in range(steps):
        g = styblinski_tang_grad(*theta)
        v = beta * v - eta * g
        theta = theta + v
        path.append(theta.copy())
    return np.array(path)


def run_adagrad(theta0, eta=0.40, eps=1e-8, steps=1200):
    theta = np.array(theta0, float)
    r = np.zeros_like(theta)
    path = [theta.copy()]
    for _ in range(steps):
        g = styblinski_tang_grad(*theta)
        r = r + g * g
        lr_eff = eta / (np.sqrt(r) + eps)
        theta = theta - lr_eff * g
        path.append(theta.copy())
    return np.array(path)

def run_rmsprop(theta0, eta=1e-2, rho=0.9, eps=1e-8, steps=1200):
    """
    s_t = rho * s_{t-1} + (1 - rho) * g_t^2
    theta <- theta - eta * g_t / (sqrt(s_t) + eps)
    """
    theta = np.array(theta0, float)
    s = np.zeros_like(theta)
    path = [theta.copy()]
    for step in range(steps):
        g = styblinski_tang_grad(*theta)
        s = rho * s + (1 - rho) * (g * g)
        theta = theta - eta * g / (np.sqrt(s) + eps)
        path.append(theta.copy())
    return np.array(path)

def run_rmsprop_centered(theta0, eta=1e-2, rho=0.9, eps=1e-8, steps=1200):
    """
    m_t = rho * m_{t-1} + (1 - rho) * g_t
    s_t = rho * s_{t-1} + (1 - rho) * g_t^2
    denom = sqrt(s_t - m_t^2) + eps   # variance-based
    """
    theta = np.array(theta0, float)
    m = np.zeros_like(theta)
    s = np.zeros_like(theta)
    path = [theta.copy()]
    for _ in range(steps):
        g = styblinski_tang_grad(*theta)
        m = rho * m + (1 - rho) * g
        s = rho * s + (1 - rho) * (g * g)
        denom = np.sqrt(np.maximum(s - m * m, 0.0)) + eps
        theta = theta - eta * g / denom
        path.append(theta.copy())
    return np.array(path)

def run_adam(theta0, eta=1e-2, beta1=0.9, beta2=0.999, eps=1e-8, steps=1200):
    theta = np.array(theta0, float)
    m = np.zeros_like(theta)
    v = np.zeros_like(theta)
    path = [theta.copy()]
    for t in range(1, steps + 1):
        g = styblinski_tang_grad(*theta)
        m = beta1 * m + (1 - beta1) * g
        v = beta2 * v + (1 - beta2) * (g * g)
        m_hat = m / (1 - beta1**t)
        v_hat = v / (1 - beta2**t)
        theta = theta - eta * m_hat / (np.sqrt(v_hat) + eps)
        path.append(theta.copy())
    return np.array(path)

theta_start = np.array([4.1, 4.5], dtype=float)
steps = 1200

eta_sgd = 0.02
eta_mom, beta = 0.02, 0.90
eta_adagrad = 0.40
eta_rms, rho, eps = 1e-2, 0.9, 1e-8
eta_rms_c = 1e-2

sgd_path = run_sgd(theta_start, eta=eta_sgd, steps=steps)
mom_path = run_momentum(theta_start, eta=eta_mom, beta=beta, steps=steps)
ada_path = run_adagrad(theta_start, eta=eta_adagrad, steps=steps)
rms_path = run_rmsprop(theta_start, eta=eta_rms, rho=rho, eps=eps, steps=steps)
rmsc_path = run_rmsprop_centered(theta_start, eta=eta_rms_c, rho=rho, eps=eps, steps=steps)
adam_path = run_adam(theta_start)
mins2d, gmin_pt, gmin_val = stationary_points_and_global_min()

x = y = np.linspace(-5, 5, 400)
X, Y = np.meshgrid(x, y)
Z = styblinski_tang_fn(X, Y)

plt.figure(figsize=(9, 8))
cs = plt.contour(X, Y, Z, levels=50, alpha=0.85)
plt.clabel(cs, inline=True, fmt="%.0f", fontsize=7)

plt.plot(sgd_path[:, 0], sgd_path[:, 1], '.-', lw=1.2, ms=3, label='SGD')
plt.plot(mom_path[:, 0], mom_path[:, 1], '.-', lw=1.2, ms=3, label=f'Momentum (β={beta})')
plt.plot(ada_path[:, 0], ada_path[:, 1], '.-', lw=1.2, ms=3, label='AdaGrad')
plt.plot(rms_path[:, 0], rms_path[:, 1], '.-', lw=1.2, ms=3, label=f'RMSProp (ρ={rho})')
plt.plot(rmsc_path[:, 0], rmsc_path[:, 1], '.-', lw=1.2, ms=3, label='RMSProp (centered)')
plt.plot(adam_path[:, 0], adam_path[:, 1], '.-', lw=1.2, ms=3, label='Adam')

plt.scatter(sgd_path[0, 0], sgd_path[0, 1], s=80, label='Start', zorder=3)
plt.scatter(sgd_path[-1, 0], sgd_path[-1, 1], s=60, label='SGD End', zorder=3)
plt.scatter(mom_path[-1, 0], mom_path[-1, 1], s=60, label='Momentum End', zorder=3)
plt.scatter(ada_path[-1, 0], ada_path[-1, 1], s=60, label='AdaGrad End', zorder=3)
plt.scatter(rms_path[-1, 0], rms_path[-1, 1], s=60, label='RMSProp End', zorder=3)
plt.scatter(rmsc_path[-1, 0], rmsc_path[-1, 1], s=60, label='RMSProp (centered) End', zorder=3)
plt.scatter(adam_path[-1, 0], adam_path[-1, 1], s=60, label='Adam End', zorder=3)

vals = np.array([styblinski_tang_fn(x0, y0) for x0, y0 in mins2d])
mask = np.ones(len(mins2d), dtype=bool)
mask[np.argmin(vals)] = False
if np.any(mask):
    plt.scatter(mins2d[mask, 0], mins2d[mask, 1],
                marker='v', s=120, edgecolor='k', facecolor='white',
                label='Local minima', zorder=4)
plt.scatter(gmin_pt[0], gmin_pt[1], marker='*', s=220, edgecolor='k',
            facecolor='gold', label=f'Global min ({gmin_pt[0]:.4f}, {gmin_pt[1]:.4f})\n f={gmin_val:.4f}', zorder=5)

plt.title("SGD vs Momentum vs AdaGrad vs RMSProp (and Centered) on Styblinski–Tang")
plt.xlabel("x")
plt.ylabel("y")
plt.legend(loc='upper left')
plt.grid(alpha=0.3)
plt.tight_layout()
plt.show()

Weight Decay Coupling (the “W” in AdamW, 2017)

A very slight distinction but this was a key change that led to better generalization. AdamW was utilized to train BERT, GPT, and others. Most modern frameworks (PyTorch, Tensorflow, JAX) now make it the default.

L2 Regularization

Ok so before we get to AdamW cleanly, we have to discuss L2 regularization (also commonly noted as $\lambda | \theta | ^2 $). The idea with L2 regularization is that we have a penalty on our loss function so that the model doesn’t overfit. Basically saying we want to minimize both the loss and the size of the weights.

When you use Adam, you compute the gradient of your total loss. So basically from start to finish, walking through:

\[\begin{align} L_{total} ( \theta ) &= L_{data} (\theta) + \frac{\lambda}{2} \| \theta \|^2 \\ \nabla_{\theta} L_{total} (\theta) &= \nabla_{\theta} L_{data} (\theta) + \lambda \theta \end{align}\]

This means that every gradient update has two parts:

1. a data term
2. a regularization term

And again, so $\lambda$ is the regularization strength - basically how much we want to penalize large weights.

So now incorporating this into Adam. We normally compute the gradient of our total loss.

\[g_t = \nabla_{\theta} L_{total} (\theta_t) = \nabla_{\theta} L_{data} (\theta_t) + \lambda \theta_t\]

But the downside is that the $+ \lambda \theta_t$ term becomes part of the gradient update…. That’s an issue for us because Adam does its adaptive scaling magic:

\[\theta_{t+1} = \theta_{t} - \eta \frac{\hat{m}_t}{\sqrt{\hat{v}_t} + \varepsilon}\]

but that adaptive scaling portion also now includes the $\lambda \theta_t$ portion meaning some weights get decayed more than others, all depending on their individual $v_t$ values.

Knowledge check

Let's say we're not applying L2 regularization as part of our loss function, is AdamW going to be different at all from Adam?

Select the answer

1. No, L2 regularization is linked to AdamW so if it isn't in our loss function, then we don't need AdamW
2. Yes, it can still be beneficial

Here’s another one. And look at how we can call the AdamW optimizer in pytorch:

optimizer = torch.optim.AdamW(model.parameters(), lr=learning_rate, weight_decay=this_is_equiv_to_lambda)

Knowledge check

If I explicitly wanted to use Adam instead of AdamW, can I modify (and if so, how could I) the above pytorch code to get that?

Select the answer

1. trick question! you can't
2. yes, there's another AdamW parameter in pytorch that enables vanilla Adam
3. yes,we can change the weight_decay

Viz

import numpy as np
import matplotlib.pyplot as plt
from itertools import product
from sympy import Matrix
from IPython.display import display

def styblinski_tang_fn(x: float, y: float) -> float:
    return 0.5 * ((x**4 - 16 * x**2 + 5 * x) + (y**4 - 16 * y**2 + 5 * y))

def styblinski_tang_grad(x: float, y: float) -> np.ndarray:
    dfx = 2 * x**3 - 16 * x + 2.5
    dfy = 2 * y**3 - 16 * y + 2.5
    return np.array([dfx, dfy], dtype=float)

def stationary_points_and_global_min():
    roots = np.roots([2.0, 0.0, -16.0, 2.5])
    roots = np.real(roots[np.isreal(roots)])
    minima_1d = [r for r in roots if (6 * r * r - 16) > 0]
    mins2d = np.array(list(product(minima_1d, repeat=2)), dtype=float)
    vals = np.array([styblinski_tang_fn(x, y) for x, y in mins2d])
    gidx = np.argmin(vals)
    return mins2d, mins2d[gidx], vals[gidx]

def run_sgd(theta0, eta=0.02, steps=1200):
    theta = np.array(theta0, float)
    path = [theta.copy()]
    for _ in range(steps):
        theta -= eta * styblinski_tang_grad(*theta)
        path.append(theta.copy())
    return np.array(path)

def run_momentum(theta0, eta=0.02, beta=0.90, steps=1200):
    theta = np.array(theta0, float)
    v = np.zeros_like(theta)
    path = [theta.copy()]
    for _ in range(steps):
        g = styblinski_tang_grad(*theta)
        v = beta * v - eta * g
        theta = theta + v
        path.append(theta.copy())
    return np.array(path)

def run_adagrad(theta0, eta=0.40, eps=1e-8, steps=1200):
    theta = np.array(theta0, float)
    r = np.zeros_like(theta)
    path = [theta.copy()]
    for _ in range(steps):
        g = styblinski_tang_grad(*theta)
        r = r + g * g
        lr_eff = eta / (np.sqrt(r) + eps)
        theta = theta - lr_eff * g
        path.append(theta.copy())
    return np.array(path)

def run_rmsprop(theta0, eta=1e-2, rho=0.9, eps=1e-8, steps=1200):
    """
    s_t = rho * s_{t-1} + (1 - rho) * g_t^2
    theta <- theta - eta * g_t / (sqrt(s_t) + eps)
    """
    theta = np.array(theta0, float)
    s = np.zeros_like(theta)
    path = [theta.copy()]
    for step in range(steps):
        g = styblinski_tang_grad(*theta)
        s = rho * s + (1 - rho) * (g * g)
        theta = theta - eta * g / (np.sqrt(s) + eps)
        path.append(theta.copy())
    return np.array(path)

def run_rmsprop_centered(theta0, eta=1e-2, rho=0.9, eps=1e-8, steps=1200):
    """
    m_t = rho * m_{t-1} + (1 - rho) * g_t
    s_t = rho * s_{t-1} + (1 - rho) * g_t^2
    denom = sqrt(s_t - m_t^2) + eps   # variance-based
    """
    theta = np.array(theta0, float)
    m = np.zeros_like(theta)
    s = np.zeros_like(theta)
    path = [theta.copy()]
    for _ in range(steps):
        g = styblinski_tang_grad(*theta)
        m = rho * m + (1 - rho) * g
        s = rho * s + (1 - rho) * (g * g)
        denom = np.sqrt(np.maximum(s - m * m, 0.0)) + eps
        theta = theta - eta * g / denom
        path.append(theta.copy())
    return np.array(path)

def run_adam(theta0, eta=1e-2, beta1=0.9, beta2=0.999, eps=1e-8, steps=1200):
    theta = np.array(theta0, float)
    m = np.zeros_like(theta)
    v = np.zeros_like(theta)
    path = [theta.copy()]
    for t in range(1, steps + 1):
        g = styblinski_tang_grad(*theta)
        m = beta1 * m + (1 - beta1) * g
        v = beta2 * v + (1 - beta2) * (g * g)
        m_hat = m / (1 - beta1**t)
        v_hat = v / (1 - beta2**t)
        theta = theta - eta * m_hat / (np.sqrt(v_hat) + eps)
        path.append(theta.copy())
    return np.array(path)

def run_adamw(theta0, eta=1e-2, beta1=0.9, beta2=0.999, eps=1e-8, weight_decay=0.01, steps=1200):
    """
    AdamW: decoupled weight decay
      theta <- theta - eta * ( m_hat / (sqrt(v_hat)+eps) )  # adaptive step
      theta <- theta - eta * weight_decay * theta           # uniform shrink
    Note: setting weight_decay=0.0 makes AdamW identical to Adam.
    """
    theta = np.array(theta0, float)
    m = np.zeros_like(theta)
    v = np.zeros_like(theta)
    path = [theta.copy()]
    for t in range(1, steps + 1):
        g = styblinski_tang_grad(*theta)
        m = beta1 * m + (1 - beta1) * g
        v = beta2 * v + (1 - beta2) * (g * g)
        m_hat = m / (1 - beta1**t)
        v_hat = v / (1 - beta2**t)

        # adaptive update
        theta = theta - eta * (m_hat / (np.sqrt(v_hat) + eps))
        # decoupled weight decay (uniform; not scaled by v_hat)
        theta = theta - eta * weight_decay * theta

        path.append(theta.copy())
    return np.array(path)

# ----- params -----
theta_start = np.array([4.1, 4.5], dtype=float)
steps = 1200

eta_sgd = 0.02
eta_mom, beta = 0.02, 0.90
eta_adagrad = 0.40
eta_rms, rho, eps = 1e-2, 0.9, 1e-8
eta_rms_c = 1e-2

# Adam / AdamW hyperparams
eta_adam = 1e-2
beta1, beta2 = 0.9, 0.999
eps_adam = 1e-8
wd = 1e-2     # try 0.0 (Adam-equivalent) vs 1e-3 vs 1e-2

# ----- runs -----
sgd_path  = run_sgd(theta_start, eta=eta_sgd, steps=steps)
mom_path  = run_momentum(theta_start, eta=eta_mom, beta=beta, steps=steps)
ada_path  = run_adagrad(theta_start, eta=eta_adagrad, steps=steps)
rms_path  = run_rmsprop(theta_start, eta=eta_rms, rho=rho, eps=eps, steps=steps)
rmsc_path = run_rmsprop_centered(theta_start, eta=eta_rms_c, rho=rho, eps=eps, steps=steps)
adam_path = run_adam(theta_start, eta=eta_adam, beta1=beta1, beta2=beta2, eps=eps_adam, steps=steps)
adamw_path = run_adamw(theta_start, eta=eta_adam, beta1=beta1, beta2=beta2, eps=eps_adam, weight_decay=wd, steps=steps)

mins2d, gmin_pt, gmin_val = stationary_points_and_global_min()

# ----- viz -----
x = y = np.linspace(-5, 5, 400)
X, Y = np.meshgrid(x, y)
Z = styblinski_tang_fn(X, Y)

plt.figure(figsize=(9, 8))
cs = plt.contour(X, Y, Z, levels=50, alpha=0.85)
plt.clabel(cs, inline=True, fmt="%.0f", fontsize=7)

plt.plot(sgd_path[:, 0],   sgd_path[:, 1],   '.-', lw=1.2, ms=3, label='SGD')
plt.plot(mom_path[:, 0],   mom_path[:, 1],   '.-', lw=1.2, ms=3, label=f'Momentum (β={beta})')
plt.plot(ada_path[:, 0],   ada_path[:, 1],   '.-', lw=1.2, ms=3, label='AdaGrad')
plt.plot(rms_path[:, 0],   rms_path[:, 1],   '.-', lw=1.2, ms=3, label=f'RMSProp (ρ={rho})')
plt.plot(rmsc_path[:, 0],  rmsc_path[:, 1],  '.-', lw=1.2, ms=3, label='RMSProp (centered)')
plt.plot(adam_path[:, 0],  adam_path[:, 1],  '.-', lw=1.2, ms=3, label='Adam')
plt.plot(adamw_path[:, 0], adamw_path[:, 1], '.-', lw=1.2, ms=3, label=f'AdamW (wd={wd})')

plt.scatter(sgd_path[0, 0], sgd_path[0, 1], s=80, label='Start', zorder=3)
plt.scatter(sgd_path[-1, 0], sgd_path[-1, 1], s=60, label='SGD End', zorder=3)
plt.scatter(mom_path[-1, 0], mom_path[-1, 1], s=60, label='Momentum End', zorder=3)
plt.scatter(ada_path[-1, 0], ada_path[-1, 1], s=60, label='AdaGrad End', zorder=3)
plt.scatter(rms_path[-1, 0], rms_path[-1, 1], s=60, label='RMSProp End', zorder=3)
plt.scatter(rmsc_path[-1, 0], rmsc_path[-1, 1], s=60, label='RMSProp (centered) End', zorder=3)
plt.scatter(adam_path[-1, 0], adam_path[-1, 1], s=60, label='Adam End', zorder=3)
plt.scatter(adamw_path[-1, 0], adamw_path[-1, 1], s=60, label='AdamW End', zorder=3)

plt.scatter(gmin_pt[0], gmin_pt[1], marker='*', s=220, edgecolor='k',
            facecolor='gold', label=f'Global min ({gmin_pt[0]:.4f}, {gmin_pt[1]:.4f})\n f={gmin_val:.4f}', zorder=5)

vals = np.array([styblinski_tang_fn(x0, y0) for x0, y0 in mins2d])
mask = np.ones(len(mins2d), dtype=bool)
mask[np.argmin(vals)] = False
if np.any(mask):
    plt.scatter(mins2d[mask, 0], mins2d[mask, 1],
                marker='v', s=120, edgecolor='k', facecolor='white',
                label='Local minima', zorder=4)

plt.title("SGD, Momentum, AdaGrad, RMSProp (+centered), Adam, AdamW on Styblinski–Tang")
plt.xlabel("x"); plt.ylabel("y")
plt.legend(loc='upper left')
plt.grid(alpha=0.3)
plt.tight_layout()
plt.show()

You’ll note… before we get to Muon that this example is almost entirely contrived. While the Styblinski-Tang function is a good example of a loss function that would be easy to get caught in a local minima and is hard to find the global min, you’ll note that just because in my contrived examples the SGD with Momentum optimizer is finding the global min does not mean that it generalizes well. Generally AdamW has been the defacto winner.

Muon (MomentUm Orthogonalized by Newton-Schulz) (2025)

Alright jeez, all of the above was a bit accidental, but I wanted to give you all a build up / very very quick run through of the various optimziers that have evolved. Again, the space is definitely iterative (pun intended), but these optimizers all build off of each other. Muon is no different.

Theory

The idea is that we’re still working with our momentum matrix. The momentum matrix can tend to become row-rank in practice, which means only a couple of directions dominate.

Muon tries to orthogonalize our momentum matrix. Rare directions are amplified by the orthogonalization. Again, recall from the Little Book of Linear Algebra that this means:

\(\text{Ortho}(M) = \text{argmin}_O \{ \| O - M \| f \}\) where $OO^T = I$ and $O^T O = I$

Ok while this is hard… what do we turn to besides our good friend - the swiss army knife of linalg - SVD (singular value decomposiiton)

\[M = U S V^T\]

So we would compute SVD and then we’d set the S matrix to be diag(1).

However, once again SVD is computationally expensive so this

Odd Polynomial Matrix

Odd polynomial matrices are:

\[\rho (X) = aX + b(X X^T)X\]

so we could do:

\[\rho (M) = aM + b(MM^T)M\]

So let’s go ahead and do some math where we substitute in $M$.

\[\begin{aligned} \rho (M) &= aM + b(MM^T)M \\ \rho (M) &= (a + b(MM^T))M \\ \rho (M) &= (a + b((USV^T)(VSU^T)))(USV^T) \\ \rho (M) &= (a + b(USV^TVSU^T))(USV^T) \\ \\ &\quad \text{because $V$ is orthonormal, $V^TV = I$} \\ \\ \rho (M) &= (a + b(USSU^T))(USV^T) \\ \\ &\quad \text{and $S$ is diagonal so $SS = S^2$} \\ \\ \rho (M) &= (a + b(US^2U^T))(USV^T) \\ \rho (M) &= a(USV^T) + b(US^2U^TUSV^T) \\ \\ &\quad \text{because $U$ is orthonormal, $U^TU = I$} \\ \\ \rho (M) &= a(USV^T) + b(US^2SV^T) \\ \rho (M) &= a(USV^T) + b(US^3V^T) \\ \\ &\quad \text{simplifying gives} \\ \\ \rho (M) &= U(aS + bS^3)V^T \end{aligned}\]

So… **applying an odd polynomial matrix function to M acts on the singular values in the same way as applying the function to each singular value function individually and then reconstructing the original matrix from the functions).

This expands for odd polynomials so just take this for granted or derive it for yourself:

\[\begin{align} \rho (M) &= aM + b(MM^T)M + c(MM^T)^2 M \\ \vdots \\ \rho (M) &= U(aS + bS^3 + cS^5)V^T \\ \end{align}\]

Again, we want S to be diag with 1s… So this now becomes an optimization problem within itself. We’re trying to pick the coefficients of $a, b, c$ so that we get S = np.eye(S.shape[0]).

So how do we pick out the best parameters that will help us do that….

Newton-Schulz Iteration

Again, this video is fantastic. However, this part was a little too abstracted. We’ll turn back to manim here for some more helpful visualizations and understanding.

~So I’m going to dive into the derivation here.~ Actually, it’s very interesting and I’m going to cover in another blog post. I’ll link it here.

For now, assume that we have these params:

• $a = 3.4445$
• $b = -4.7775$
• $c = 2.0315$

and those are going to be the params of our newton-schulz iteration that help us converge to what we consider is a valid $S$ for the singular values part of the SVD that has eigenvalues close-ish to 1.

Overview

So now we have:

for step in steps:
    compute gradient 
    compute momentum
    normalize momentum matrix
    orthogonalization
    update parameters

Now there is also muon with a weight adjustement similar to what we did with AdamW.

So we have:

\[\begin{align} G_t &\leftarrow \nabla L_t (\theta_{t-1}) \\ M_t &\leftarrow \beta M_{t-1} + G_t \\ M'_t &\leftarrow \frac{M_t}{\| M_t \|_F} \\ O_t &\leftarrow \text{NewtonSchulz5}(M'_t) \\ \theta_t &\leftarrow \theta_{t-1} - \alpha \left(0.2 \sqrt{\text{max}(n,m)} \cdot O_t + \lambda \theta_{t-1}\right) \end{align}\]

Implementation

I actually want to introduce this section by looking at PyTorch’s documentation. This was added recently, but let’s look here:

This should look super familiar to the code that we’ve been covering!! The only tricky part is the AdjustLR step which deviates slightly between what the video / I have above covers (which is Moonshot’s implementation) vs Jordan Keller’s original impl of $sqrt{\text{max}(1, \frac{B}{A})}$.

There are a couple of tricky parts with implementing this:

def newton_schulz_5(M_matrix, steps=5, eps=1e-7):
    a, b, c = (3.4445, -4.7750, 2.0315) # from Keller Jordan
    X = M_matrix.astype(np.float32, copy=False) # speed up in practice
    
    if X.shape[0] > X.shape[1]:
        X = X.T

    X = X / (np.linalg.norm(X) + eps) # frobenius norm by def
    # so this is tricky but we're looking here
    # \rho (M) &= aM + b(MM^T)M + c(MM^T)^2 M
    for _ in range(steps):
        A = X @ X.T
        B = b * A + c * A @ A
        X = a * X + B @ X
    if X.shape[0] > X.shape[1]:
        X = X.T
    return X


def run_muon_muonshot(theta0, eta=1e-2, beta=0.95, weight_decay=1e-2, steps=1200,
             ns_steps=5, eps=1e-7, use_nesterov=True):
    theta = np.array(theta0, float)
    if theta.ndim == 1:
        theta = theta[:, None]
    elif theta.shape[0] == 1 and theta.shape[1] > 1:
        theta = theta.T

    def adjust_lr(A, B):
        return 0.2 * np.sqrt(float(max(A, B)))

    A, B = theta.shape
    path = [theta.copy()]
    B_momentum_buffer = np.zeros_like(theta)
    for _ in range(steps):
        g = styblinski_tang_grad(*theta)  
        B_momentum_buffer = beta * B_momentum_buffer + g
        # didn't cover nestorv but pytorch has it
        M_eff = g + beta * B_momentum_buffer if use_nesterov else B_momentum_buffer
        O = newton_schulz_5(M_eff, steps=ns_steps, eps=eps)
        # decoupled weight decay (uniform shrink)
        theta = theta - eta * (adjust_lr(A, B) * O + weight_decay * theta)
        path.append(theta.copy())

    return np.array(path)

Once again, here is visualization code:

import numpy as np
import matplotlib.pyplot as plt
from itertools import product
from sympy import Matrix
from IPython.display import display

def styblinski_tang_fn(x: float, y: float) -> float:
    return 0.5 * ((x**4 - 16 * x**2 + 5 * x) + (y**4 - 16 * y**2 + 5 * y))

def styblinski_tang_grad(x: float, y: float) -> np.ndarray:
    dfx = 2 * x**3 - 16 * x + 2.5
    dfy = 2 * y**3 - 16 * y + 2.5
    return np.array([dfx, dfy], dtype=float)

def stationary_points_and_global_min():
    roots = np.roots([2.0, 0.0, -16.0, 2.5])
    roots = np.real(roots[np.isreal(roots)])
    minima_1d = [r for r in roots if (6 * r * r - 16) > 0]
    mins2d = np.array(list(product(minima_1d, repeat=2)), dtype=float)
    vals = np.array([styblinski_tang_fn(x, y) for x, y in mins2d])
    gidx = np.argmin(vals)
    return mins2d, mins2d[gidx], vals[gidx]

def run_sgd(theta0, eta=0.02, steps=1200):
    theta = np.array(theta0, float)
    path = [theta.copy()]
    for _ in range(steps):
        theta -= eta * styblinski_tang_grad(*theta)
        path.append(theta.copy())
    return np.array(path)

def run_momentum(theta0, eta=0.02, beta=0.90, steps=1200):
    theta = np.array(theta0, float)
    v = np.zeros_like(theta)
    path = [theta.copy()]
    for _ in range(steps):
        g = styblinski_tang_grad(*theta)
        v = beta * v - eta * g
        theta = theta + v
        path.append(theta.copy())
    return np.array(path)

def run_adagrad(theta0, eta=0.40, eps=1e-8, steps=1200):
    theta = np.array(theta0, float)
    r = np.zeros_like(theta)
    path = [theta.copy()]
    for _ in range(steps):
        g = styblinski_tang_grad(*theta)
        r = r + g * g
        lr_eff = eta / (np.sqrt(r) + eps)
        theta = theta - lr_eff * g
        path.append(theta.copy())
    return np.array(path)

def run_rmsprop(theta0, eta=1e-2, rho=0.9, eps=1e-8, steps=1200):
    """
    s_t = rho * s_{t-1} + (1 - rho) * g_t^2
    theta <- theta - eta * g_t / (sqrt(s_t) + eps)
    """
    theta = np.array(theta0, float)
    s = np.zeros_like(theta)
    path = [theta.copy()]
    for step in range(steps):
        g = styblinski_tang_grad(*theta)
        s = rho * s + (1 - rho) * (g * g)
        theta = theta - eta * g / (np.sqrt(s) + eps)
        path.append(theta.copy())
    return np.array(path)

def run_rmsprop_centered(theta0, eta=1e-2, rho=0.9, eps=1e-8, steps=1200):
    """
    m_t = rho * m_{t-1} + (1 - rho) * g_t
    s_t = rho * s_{t-1} + (1 - rho) * g_t^2
    denom = sqrt(s_t - m_t^2) + eps   # variance-based
    """
    theta = np.array(theta0, float)
    m = np.zeros_like(theta)
    s = np.zeros_like(theta)
    path = [theta.copy()]
    for _ in range(steps):
        g = styblinski_tang_grad(*theta)
        m = rho * m + (1 - rho) * g
        s = rho * s + (1 - rho) * (g * g)
        denom = np.sqrt(np.maximum(s - m * m, 0.0)) + eps
        theta = theta - eta * g / denom
        path.append(theta.copy())
    return np.array(path)

def run_adam(theta0, eta=1e-2, beta1=0.9, beta2=0.999, eps=1e-8, steps=1200):
    theta = np.array(theta0, float)
    m = np.zeros_like(theta)
    v = np.zeros_like(theta)
    path = [theta.copy()]
    for t in range(1, steps + 1):
        g = styblinski_tang_grad(*theta)
        m = beta1 * m + (1 - beta1) * g
        v = beta2 * v + (1 - beta2) * (g * g)
        m_hat = m / (1 - beta1**t)
        v_hat = v / (1 - beta2**t)
        theta = theta - eta * m_hat / (np.sqrt(v_hat) + eps)
        path.append(theta.copy())
    return np.array(path)

def run_adamw(theta0, eta=1e-2, beta1=0.9, beta2=0.999, eps=1e-8, weight_decay=0.01, steps=1200):
    """
    AdamW: decoupled weight decay
      theta <- theta - eta * ( m_hat / (sqrt(v_hat)+eps) )  # adaptive step
      theta <- theta - eta * weight_decay * theta           # uniform shrink
    Note: setting weight_decay=0.0 makes AdamW identical to Adam.
    """
    theta = np.array(theta0, float)
    m = np.zeros_like(theta)
    v = np.zeros_like(theta)
    path = [theta.copy()]
    for t in range(1, steps + 1):
        g = styblinski_tang_grad(*theta)
        m = beta1 * m + (1 - beta1) * g
        v = beta2 * v + (1 - beta2) * (g * g)
        m_hat = m / (1 - beta1**t)
        v_hat = v / (1 - beta2**t)

        # adaptive update
        theta = theta - eta * (m_hat / (np.sqrt(v_hat) + eps))
        # decoupled weight decay (uniform; not scaled by v_hat)
        theta = theta - eta * weight_decay * theta

        path.append(theta.copy())
    return np.array(path)

def newton_schulz_5(M_matrix, steps=5, eps=1e-7):
    # from Keller Jordan
    a, b, c = (3.4445, -4.7750, 2.0315)

    # speed up in practical
    X = M_matrix.astype(np.float32, copy=False)

    transposed = False
    if X.shape[0] > X.shape[1]:
        X = X.T
        transposed = True

    # frobenius norm
    X = X / (np.linalg.norm(X) + eps)
    
    # so this is tricky but we're looking here
    # \rho (M) &= aM + b(MM^T)M + c(MM^T)^2 M
    for _ in range(steps):
        A = X @ X.T
        B = b * A + c * A @ A
        X = a * X + B @ X

    if transposed:
        X = X.T
    return X


def run_muon_muonshot(theta0, eta=1e-2, beta=0.95, weight_decay=1e-2, steps=1200,
             ns_steps=5, eps=1e-7, use_nesterov=True):

    theta = np.array(theta0, float)
    if theta.ndim == 1:
        theta = theta[:, None]          # (n,) -> (n,1)
    elif theta.shape[0] == 1 and theta.shape[1] > 1:
        theta = theta.T                 # (1,n) -> (n,1)

    def adjust_lr(A, B):
        return 0.2 * np.sqrt(float(max(A, B)))

    A, B = theta.shape

    path = [theta.copy()]
    B_momentum_buffer = np.zeros_like(theta)
    for _ in range(steps):
        g = styblinski_tang_grad(*theta)  
        B_momentum_buffer = beta * B_momentum_buffer + g
        # didn't cover nestorv but pytorch has it
        M_eff = g + beta * B_momentum_buffer if use_nesterov else B_momentum_buffer
        O = newton_schulz_5(M_eff, steps=ns_steps, eps=eps)
        # decoupled weight decay (uniform shrink)
        theta = theta - eta * (adjust_lr(A, B) * O + weight_decay * theta)
        path.append(theta.copy())

    return np.array(path)

# ----- params -----
theta_start = np.array([4.1, 4.5], dtype=float)
steps = 1200

eta_sgd = 0.02
eta_mom, beta = 0.02, 0.90
eta_adagrad = 0.40
eta_rms, rho, eps = 1e-2, 0.9, 1e-8
eta_rms_c = 1e-2

# Adam / AdamW hyperparams
eta_adam = 1e-2
beta1, beta2 = 0.9, 0.999
eps_adam = 1e-8
wd = 1e-2     # try 0.0 (Adam-equivalent) vs 1e-3 vs 1e-2

# ----- runs -----
sgd_path  = run_sgd(theta_start, eta=eta_sgd, steps=steps)
mom_path  = run_momentum(theta_start, eta=eta_mom, beta=beta, steps=steps)
ada_path  = run_adagrad(theta_start, eta=eta_adagrad, steps=steps)
rms_path  = run_rmsprop(theta_start, eta=eta_rms, rho=rho, eps=eps, steps=steps)
rmsc_path = run_rmsprop_centered(theta_start, eta=eta_rms_c, rho=rho, eps=eps, steps=steps)
adam_path = run_adam(theta_start, eta=eta_adam, beta1=beta1, beta2=beta2, eps=eps_adam, steps=steps)
adamw_path = run_adamw(theta_start, eta=eta_adam, beta1=beta1, beta2=beta2, eps=eps_adam, weight_decay=wd, steps=steps)

# ===== Muon (minimal integration; assumes your run_muon_muonshot handles shape) =====
eta_muon = 1e-2
beta_mu = 0.95
wd_mu = 1e-2
ns_steps = 5
eps_ns = 1e-7
use_nesterov = True

muon_path_raw = run_muon_muonshot(
    theta_start,
    eta=eta_muon,
    beta=beta_mu,
    weight_decay=wd_mu,
    steps=steps,
    ns_steps=ns_steps,
    eps=eps_ns,
    use_nesterov=use_nesterov
)
muon_path = muon_path_raw.squeeze(-1) if muon_path_raw.ndim == 3 else muon_path_raw  # (T,2,1) -> (T,2)

mins2d, gmin_pt, gmin_val = stationary_points_and_global_min()

# ----- viz -----
x = y = np.linspace(-5, 5, 400)
X, Y = np.meshgrid(x, y)
Z = styblinski_tang_fn(X, Y)

plt.figure(figsize=(9, 8))
cs = plt.contour(X, Y, Z, levels=50, alpha=0.85)
plt.clabel(cs, inline=True, fmt="%.0f", fontsize=7)

plt.plot(sgd_path[:, 0],   sgd_path[:, 1],   '.-', lw=1.2, ms=3, label='SGD')
plt.plot(mom_path[:, 0],   mom_path[:, 1],   '.-', lw=1.2, ms=3, label=f'Momentum (β={beta})')
plt.plot(ada_path[:, 0],   ada_path[:, 1],   '.-', lw=1.2, ms=3, label='AdaGrad')
plt.plot(rms_path[:, 0],   rms_path[:, 1],   '.-', lw=1.2, ms=3, label=f'RMSProp (ρ={rho})')
plt.plot(rmsc_path[:, 0],  rmsc_path[:, 1],  '.-', lw=1.2, ms=3, label='RMSProp (centered)')
plt.plot(adam_path[:, 0],  adam_path[:, 1],  '.-', lw=1.2, ms=3, label='Adam')
plt.plot(adamw_path[:, 0], adamw_path[:, 1], '.-', lw=1.2, ms=3, label=f'AdamW (wd={wd})')

# Muon trace (minimal additional plotting)
plt.plot(muon_path[:, 0],  muon_path[:, 1],  '.-', lw=1.4, ms=3, label=f'Muon (NS={ns_steps}, β={beta_mu})')
plt.scatter(muon_path[-1, 0],  muon_path[-1, 1],  s=60, label='Muon End', zorder=3)

plt.scatter(sgd_path[0, 0], sgd_path[0, 1], s=80, label='Start', zorder=3)
plt.scatter(sgd_path[-1, 0], sgd_path[-1, 1], s=60, label='SGD End', zorder=3)
plt.scatter(mom_path[-1, 0], mom_path[-1, 1], s=60, label='Momentum End', zorder=3)
plt.scatter(ada_path[-1, 0], ada_path[-1, 1], s=60, label='AdaGrad End', zorder=3)
plt.scatter(rms_path[-1, 0], rms_path[-1, 1], s=60, label='RMSProp End', zorder=3)
plt.scatter(rmsc_path[-1, 0], rmsc_path[-1, 1], s=60, label='RMSProp (centered) End', zorder=3)
plt.scatter(adam_path[-1, 0],  adam_path[-1, 1],  s=60, label='Adam End', zorder=3)
plt.scatter(adamw_path[-1, 0], adamw_path[-1, 1], s=60, label='AdamW End', zorder=3)

plt.scatter(gmin_pt[0], gmin_pt[1], marker='*', s=220, edgecolor='k',
            facecolor='gold', label=f'Global min ({gmin_pt[0]:.4f}, {gmin_pt[1]:.4f})\n f={gmin_val:.4f}', zorder=5)

vals = np.array([styblinski_tang_fn(x0, y0) for x0, y0 in mins2d])
mask = np.ones(len(mins2d), dtype=bool)
mask[np.argmin(vals)] = False
if np.any(mask):
    plt.scatter(mins2d[mask, 0], mins2d[mask, 1],
                marker='v', s=120, edgecolor='k', facecolor='white',
                label='Local minima', zorder=4)

plt.title("SGD, Momentum, AdaGrad, RMSProp (+centered), Adam, AdamW, Muon on Styblinski–Tang")
plt.xlabel("x"); plt.ylabel("y")
plt.legend(loc='upper left')
plt.grid(alpha=0.3)
plt.tight_layout()
plt.show()

Conclusion

Ok! I hope you have learned something. There is obviously a ton more I could write about here, but I think getting into actually writing the code and understanding the paths that we’re taking and this very detailed stepthrough is helpful. Muon is very interesting and while it’s still pretty hotly debated if it’ll scale (despite Kimi being trained on it with 1T tokens), there will be more research that certainly goes into this area.

I’m hoping to dive more into the Newton-Schulz iteration and have some interesting visualizations there, but as always, this has burned more of my time that maybe I should have allocated.