Recently, I did an interview. I got absolutely flamed and one of the reasons was I wasn’t familiar with a Disjoint Union Set (and I certainly couldn’t complete the C++ interview in time building this data structure naturally).

I figure I would go back to this and do a deeper dive because I wasn’t as familiar with it.

Table of Contents
Theory
- What is a Disjoint Set?
  - Trees
  - Forests
Example Usage
- Kruskal’s Algo for MST
The Problem
- Disjoint Set Operations
Visualization
Optimizations
- Path Compression
- Union by Rank
Rust Implementation

Theory

What is a Disjoint Set?

A disjoint set or union find or disjoint union set are all the same data structure. It is a data structure that is optimized for handling various set operations and mainly focuses on two methods: union and find (hence one of the names).

The whole goal is: detecting if a member is in a set, and if sets are connected in a fast and performant manner.

So we’ll mainly have a target set. We’re representing each subset as an inverted tree (i.e. all the child nodes are pointing back to the root).

Trees

As a reminder, trees are a specific form of a graph where:

undirected
at most 1 path between any 2 nodes
acyclic

Two types: out-tree and in-tree.

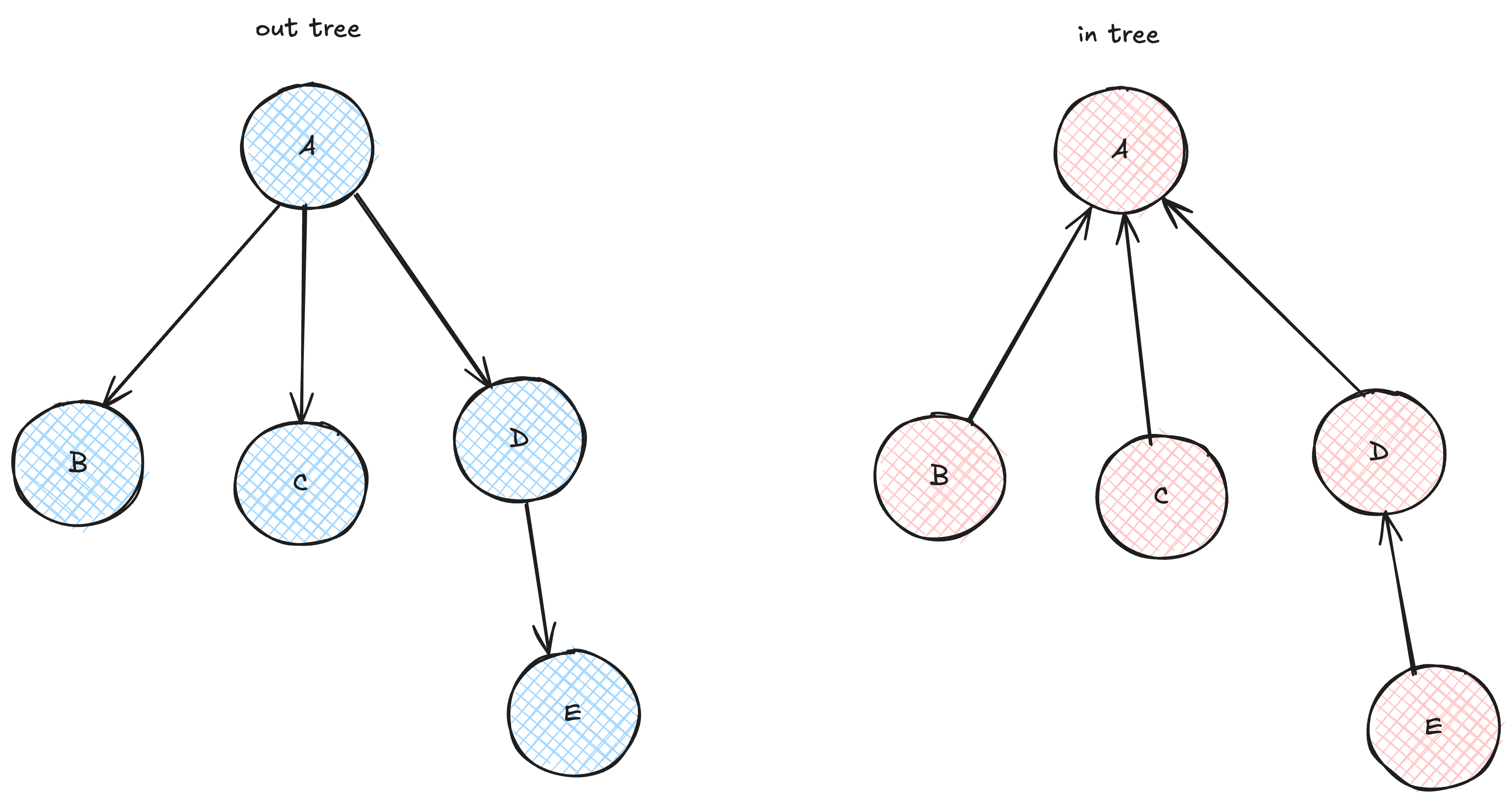
tree-types

Out-trees are probably the most common, but we’re going to be focusing on an in-tree.

Forests

A forest is a collection of trees. It’s an undirected acyclic graph, where each connected component is a tree. It’s a disjoint union of trees.

Example Usage

Kruskal’s Algo for MST

Kruskal’s algorithm is a way of detecting a minimum-spanning-tree. In a very basic phrasing, a minimum spanning tree is a subset of the edges of a connected, undirected graph that connects all the nodes. Basically, we want one “connected component” (that normally also minimizes cost).

Imagine building a road and we’re trying to build a road that hits all of our target cities but in the cheapest way (might not be best).

Kruskal’s is basically:

Sort edges (by weight)
Pick cheapest edge (if no cycle created)
Continue while MST is not complete

This greedy algorithm utilizes DSUs when we need to see if we are going to have a cycle (this is done by a disjoint set .find call).

Basically, in very lightweight pseudocode:

for edge in sorted_edges:
    if find(edge.u) != find(edge.v):
        mst.append(edge)
        union(edge.u, edge.v)

The Problem

Again, how do we check subset membership between $x$ and $y$ fast? The answer is obviously DSUs.

Disjoint Set Operations

And so with that, this data structure is going to have:

Create a new set
Find an item’s set representative (basically like the root of the subset tree)
Union, merge subsets

Creating a new set

class DisjointSet:
  def __init__(self) -> None:
    self.parent = {}

  def make_set(self, x: int) -> None:
    self.parent[x] = x

Find an item’s representative

How can we rapidly check if two targets are in the same subset? This is the whole point of the data structure basically. This is where we climb up the tree. This allows for very fast access.

class DisjointSet:
  def find(self, x: int) -> None:
    if self.parent.get(x) == x:
      return x
    return self.find(self.parent[x])

Union / merge subsets

class DisjointSet:
  def union(self, x: int, y: int) -> None:
    root_x = self.find(x)
    root_y = self.find(y)

    # only merge if x and y are not in the same set
    if root_x != root_y:
      self.parent[root_y] = root_x

Basically just stitching these subsets together. We just reset the parent for $y$ or for $x$ and that’s how we get around it.

Visualization

I thought about having Claude spin up a visualizer, but didn’t seem worth it. There are lots of good resources. The best I’ve seen is here at visualgo. There’s the visualizations / slides on the DSU here.

Optimizations

There’s two big optimizations that people generally hammer for DSUs. They are path compression and union by rank.

Path Compression

So this is a neat trick that is invoked on the find call. When we’re climbing back up the tree to roots, we “flatten” the tree along the way. We make each visited node point directly to the root. That way, the next time we do a find, it’ll take $\mathcal{O}(1)$ time. In pseudocode,

# original
def find(self, x: int) -> None:
  if self.parent[x] == x:
    return x
  return self.find(self.parent[x])

# with path compression
def find(self, x: int) -> None:
  if self.parent[x] != x:
    self.parent[x] = self.find(self.parent[x])
  return self.parent[x]

This helps keep our tree flat and wide. So for example find(5) would potentially take 5 recursive calls if we had 5 -> 4 -> 3 -> 2 -> 1, but the next find(4) would be $\mathcal{O}(1)$.

Union by Rank

This is another cool trick. When we union, we attach the smaller tree under the larger one. That once again, keeps the trees shallow so that our find operations are fast.

To do this, we keep track of rank - a measure of the tree’s height. When performing union, we compare ranks and attach smaller rank under larger rank.

class DisjointSet:
  def __init__(self) -> None:
    self.parent = {}
    self.rank = {}

  def make_set(self, x: int) -> None:
    self.parent[x] = x
    self.rank[x] = 0

  # find...
  def union(self, x: int, y: int) -> None:
    root_x = self.find(x)
    root_y = self.find(y)

    if root_x = root_y:
      return

    if self.rank[root_x] < self.rank[root_y]:
      self.parent[root_x] = root_y
    elif self.rank[root_x] > self.rank[root_y]:
      self.parent[root_y] = root_x
    else:
      self.parent[root_y] = root_x
      self.rank[root_x] += 1

So a super interesting note here though is that according to most references, rank is just used to make merging decisions. It doesn’t need to be accurate. I thought it was weird at first that we don’t bump the rank if we hit the if / elif branch…. but it is because we’re directly attaching it to the root so we know the new rank is still just going to be the bigger one. This is a very important point. Rank is almost loosely tracked but it’s a rough heuristic for the upper bound of the height.

Rust Implementation

I’ve been trying to learn more Rust given it’s everyone’s favorite programming language. So I wanted to build this up again in Rust instead of Python for learning and better management. The code is pretty readable and clean (somewhat similar to Python) so yeah I won’t describe too much else. I also put the size of each set for debugging as well.

#[derive(Debug, Clone)]
pub struct DisjointSetUnion {
    parent: Vec<usize>,
    rank: Vec<usize>,
    size: Vec<usize>,
    sets: usize,
}

impl DisjointSetUnion {
    /// create a new disjoint set union with n elements
    pub fn new(n: usize) -> Self {
        Self {
            parent: (0..n).collect(),
            rank: vec![0; n],
            size: vec![1; n],
            sets: n,
        }
    }

    /// number of disjoint sets
    pub fn num_disjoint_sets(&self) -> usize {
        self.sets
    }

    /// find the root of the set containing x
    pub fn find(&mut self, mut x: usize) -> usize {
        while self.parent[x] != x {
            let parent = self.parent[x];
            self.parent[x] = self.parent[parent];
            x = self.parent[parent];
        }
        x
    }

    /// union the sets containing x and y
    pub fn union(&mut self, x: usize, y: usize) -> usize {
        let root_x = self.find(x);
        let root_y = self.find(y);

        // same component
        if root_x == root_y {
            return root_x;
        }

        // we want smaller rank tree under higher rank tree
        // to try and keep things as flat as possible
        if self.rank[root_x] < self.rank[root_y] {
            self.parent[root_x] = root_y;
            self.size[root_y] += self.size[root_x];
            self.sets -= 1;
            return root_y;
        } else if self.rank[root_y] > self.rank[root_x] {
            self.parent[root_y] = root_x;
            self.size[root_x] += self.size[root_y];
            self.sets -= 1;
            return root_x;
        }

        //otherwise, they're equal
        self.parent[root_y] = root_x;
        self.rank[root_x] += 1;
        self.size[root_x] += self.size[root_y];
        self.sets -= 1;
        return root_x;
    }

    /// check if x and y are in the same set
    pub fn connected(&mut self, x: usize, y: usize) -> bool {
        self.find(x) == self.find(y)
    }

    /// size of the set containing x
    pub fn size_of(&mut self, x: usize) -> usize {
        // ugh perils of Rust
        // i wanted to do: self.size[self.find(x)]
        // but because the borrow checker we cannot
        // indexing into self.size immutably borrows self.size
        // and thus self for the duration of the indexing expression
        // as a result, when we do self.find we need a MUTABLE borrow
        // of self - so this conflict causes the break
        let root = self.find(x);
        self.size[root]
    }

    pub fn rank_of(&mut self, x: usize) -> usize {
        let root = self.find(x);
        self.rank[root]
    }

    // Claude added these
    /// (solely for viz) - reference to the parent array
    pub fn parent(&self) -> &[usize] {
        &self.parent
    }

    /// (solely for viz) - reference to the rank array
    pub fn rank(&self) -> &[usize] {
        &self.rank
    }

    /// (solely for viz) - reference to the size array
    pub fn size(&self) -> &[usize] {
        &self.size
    }
}

The visualization code was entirely autogenerated by Claude and then I used vhs to create the animation. Here is the demo:

demo-gif

Here is the code if you want to check it out. I’m guessing most people will just deep dive with ChatGPT which is ok too!

Disjoint Union Set

Table of Contents